Topology optimization using external mesh

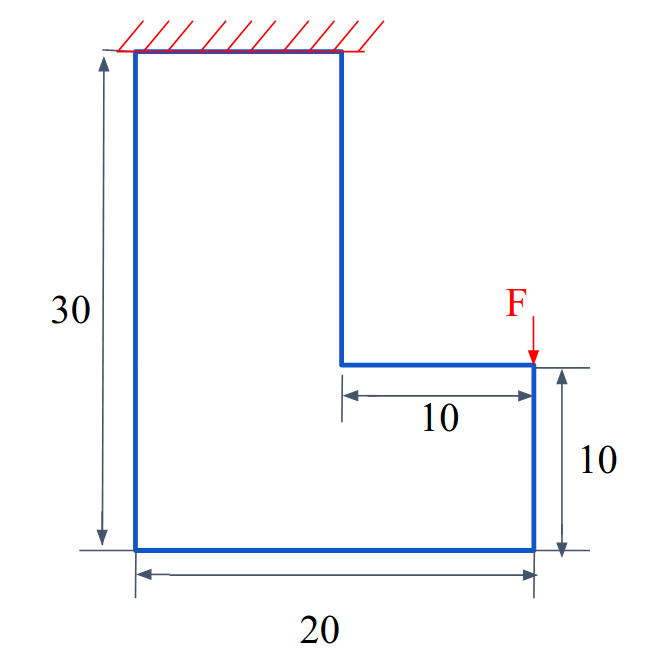
This example demonstrates a l-shape beam topology optimization using external mesh from GMSH GUI with the boundary conditions shown below. We clamp the top of the beam and apply a traction force on a few elements (two elements here) at the right corner.

../../../_images/other_1_bd.png

The variational form for the linear elastic problem is

\[\int_{\Omega}\sigma:\nabla v d x -\int_{\partial \Omega}(\sigma \cdot \eta) \cdot v d s=0 ,\]

where the \(\sigma\), \(v\) are the stress tenser and the test functions.

The code can be downloaded from here

1. Code

We explain the code in detail in this section.

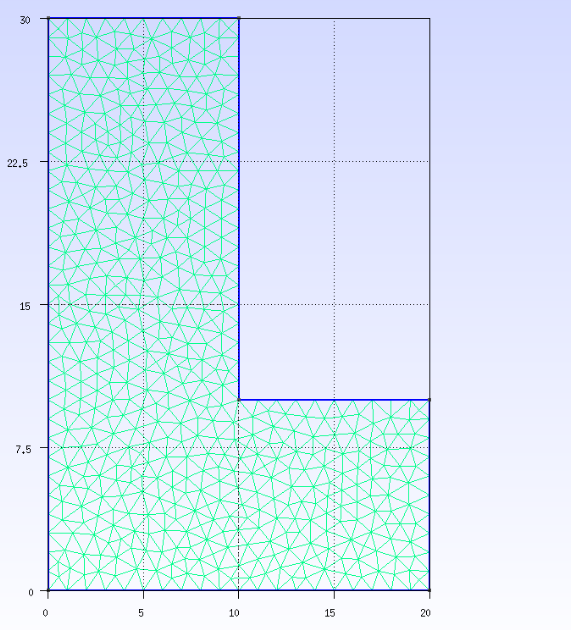
1.0. draw the mesh in GMSH

This has been explained in Steps for solving a topology optimization problem in ATOMiCS.

../../../_images/doc_gmsh_example.png

1.1. Import

First, import dolfin, numpy, openmdao, atomics.api, and atomics.pde, atomics.filter, and meshio.

import dolfin as df
import numpy as np

import openmdao.api as om

from atomics.api import PDEProblem, AtomicsGroup
from atomics.pdes.linear_elastic import get_residual_form # here we select a linear elastic PDE
from atomics.general_filter_comp import GeneralFilterComp

import meshio

1.2. Convert mesh into .xml

# import L-shaped bracket from gmsh vtk file and use meshio to convert to xml file
# (TODO: XDMF not working)
np.random.seed(0)
filename = 'test_gmsh_fine'
mesh = meshio.read(filename, file_format="vtk")
meshio.write_points_cells("fenics_mesh_l_bracket.xml", mesh.points, mesh.cells)

mesh = df.Mesh("fenics_mesh_l_bracket.xml")

1.3. Define the PDE problem

# Define the mesh and create the PDE problem
NUM_ELEMENTS_X = 80
NUM_ELEMENTS_Y = 40
LENGTH_X = 20.
LENGTH_Y = 10.
AVG_ELEMENT_SIZE = (mesh.hmax() + mesh.hmin()) / 2.

# PDE problem
pde_problem = PDEProblem(mesh)

# Add input to the PDE problem:
# name = 'density', function = density_function (function is the solution vector here)
density_function_space = df.FunctionSpace(mesh, 'DG', 0)
density_function = df.Function(density_function_space)
pde_problem.add_input('density', density_function)

# Add states to the PDE problem:
# name = 'displacements', function = displacements_function (function is the solution vector here)
# residual_form = get_residual_form(u, v, rho_e) from atomics.pdes.linear_elastic
# *inputs = density (can be multiple, here 'density' is the only input)
displacements_function_space = df.VectorFunctionSpace(mesh, 'Lagrange', 1)
displacements_function = df.Function(displacements_function_space)
v = df.TestFunction(displacements_function_space)
residual_form = get_residual_form(
    displacements_function,
    v,
    density_function,
    method='SIMP'
)

# Define traction boundary for the traction force
class TractionBoundary(df.SubDomain):
    def inside(self, x, on_boundary):
        return ((abs(x[1] - LENGTH_Y) < AVG_ELEMENT_SIZE * 2.) and
                (abs(x[0] - LENGTH_X ) < df.DOLFIN_EPS))

# Define the traction boundary
sub_domains = df.MeshFunction('size_t', mesh, mesh.topology().dim() - 1)
upper_edge = TractionBoundary()
upper_edge.mark(sub_domains, 6)
dss = df.Measure('ds')(subdomain_data=sub_domains)
f = df.Constant((0, -1. / 4 , 0.))  # define the traction force

residual_form -= df.dot(f, v) * dss(6)
pde_problem.add_state('displacements', displacements_function, residual_form, 'density')

# Add output-avg_density to the PDE problem:
volume = df.assemble(df.Constant(1.) * df.dx(domain=mesh))
avg_density_form = density_function / (df.Constant(1. * volume)) * df.dx(domain=mesh)
pde_problem.add_scalar_output('avg_density', avg_density_form, 'density')

# Add output-compliance to the PDE problem:
compliance_form = df.dot(f, displacements_function) * dss(6)
pde_problem.add_scalar_output('compliance', compliance_form, 'displacements')

# Add kinematic boundary conditions to the PDE problem:
pde_problem.add_bc(df.DirichletBC(displacements_function_space,
                    df.Constant((0.0, 0.0, 0.0)), '(abs(x[1]-30.) < DOLFIN_EPS)'))

1.4. Set up the OpenMDAO model

# Define the OpenMDAO problem and model
prob = om.Problem()
num_dof_density = pde_problem.inputs_dict['density']['function'].function_space().dim()

# Add design variables---density on each element:
comp = om.IndepVarComp()
comp.add_output(
    'density_unfiltered',
    shape=num_dof_density,
    val=np.random.random(num_dof_density) * 0.86,
)
prob.model.add_subsystem('indep_var_comp', comp, promotes=['*'])

# add the filter and specifying the filter radius--num_element_filtered=2
comp = GeneralFilterComp(density_function_space=density_function_space, num_element_filtered=2)
prob.model.add_subsystem('general_filter_comp', comp, promotes=['*'])

group = AtomicsGroup(pde_problem=pde_problem)
prob.model.add_subsystem('atomics_group', group, promotes=['*'])

prob.model.add_design_var('density_unfiltered',upper=1, lower=1e-4)
prob.model.add_objective('compliance')
prob.model.add_constraint('avg_density',upper=0.40)

if True:
    prob.driver = driver = om.pyOptSparseDriver()
    driver.options['optimizer'] = 'SNOPT'
    driver.opt_settings['Verify level'] = 0

    driver.opt_settings['Major iterations limit'] = 100000
    driver.opt_settings['Minor iterations limit'] = 100000
    driver.opt_settings['Iterations limit'] = 100000000
    driver.opt_settings['Major step limit'] = 2.0

    driver.opt_settings['Major feasibility tolerance'] = 1.0e-6
    driver.opt_settings['Major optimality tolerance'] =2.e-10
else:
    prob.driver = om.ScipyOptimizeDriver()
    prob.driver.options['optimizer'] = 'SLSQP'

prob.setup()
prob.run_model()
# prob.check_partials(compact_print=True)

# print(prob['compliance']); exit()

prob.run_driver()


#save the solution vector
df.File('solutions/displacement.pvd') << displacements_function
df.File('solutions/density_l_bracket_fine.pvd') << density_function

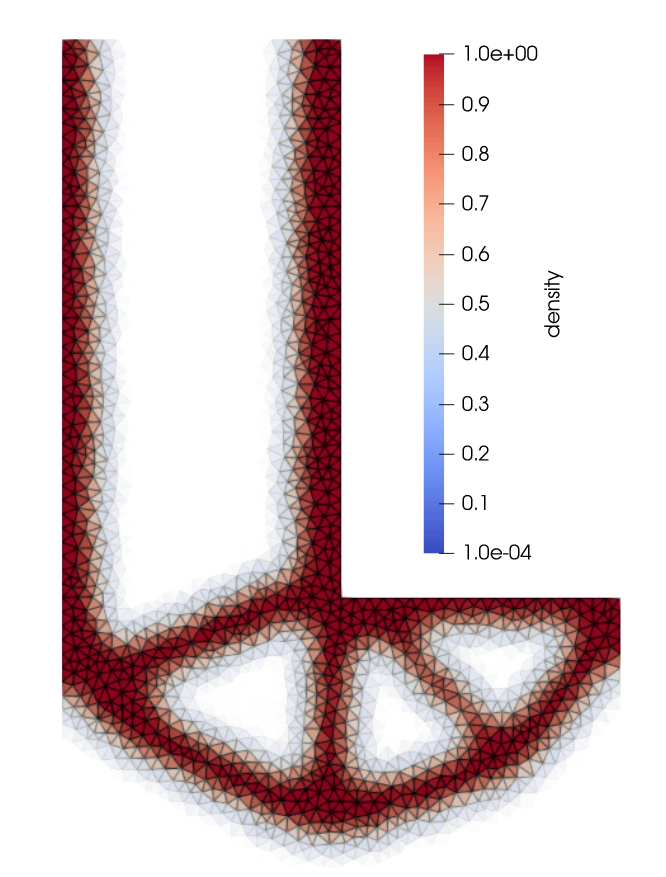
2. Results (density plot)

The users can visualize the optimized densities by opening the density_l_bracket_fine.pvd from Paraview.

../../../_images/doc_gmsh_result.png

3. Notes

If you get an error like this or your compliance is zero: *** Warning: Found no facets matching domain for boundary condition. It might happen due to the way FEniCS captures the boundary for unstructured/quadrilateral mesh. It may not capture any boundary. You can solve this by multiplying a scalar to the DOLFIN_EPS. The scalar can be determined by printing DOLFIN_EPS*scalar, this values should be less or equal to the size of one or two elements.

For example,

pde_problem.add_bc(df.DirichletBC(displacements_function_space.sub(1), df.Constant((0.0)),
                '(abs(x[1]-2.5e-2) < DOLFIN_EPS) and (abs(x[0]-2.5e-2) < DOLFIN_EPS*scalar)'))