Case study II: battery pack topology optimizations

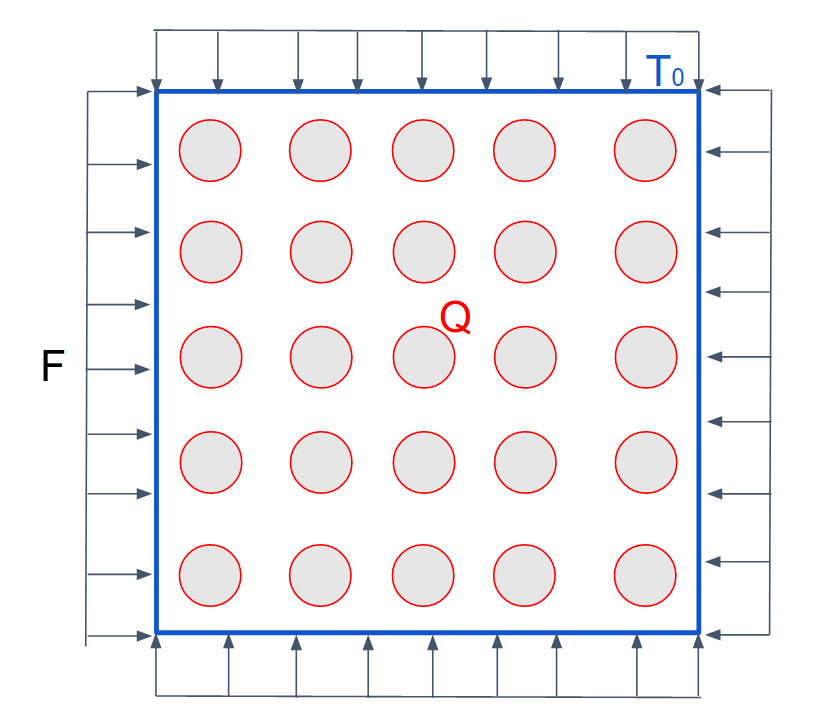
The boundary conditions for battery pack topology optimization are shown below:

We model each battery as a boundary heat flux (red ring) with a fixed temperature on the four edges of the square. We use a uniform traction load F on the four edges of the battter pack to model the load-caring functionality of the battery pack.

The variational form for the problem is

\[\int_{\Omega} \kappa \nabla T \nabla \hat{T} d x + \int_{\Omega} \sigma:\nabla v d x -\int_{\partial \Omega}\kappa(T \cdot n) \hat{T} d \partial \Omega -\int_{\partial \Omega}(\sigma \cdot \eta) \cdot v d s=0,\]

where the \(\sigma\), \(v\) are the stress tenser and the test functions for the displacements; \(T\) and \(\hat{T}\) are the function and the test functions for the temperature field.

The code can be downloaded from here

1. Code

1.1. Import

First, import dolfin, meshio, numpy, pygmsh, scipy atomics.api, atomics.pde, and atomics.general_filter_comp , as well as the stock OpenMDAO components, extract_comp, and ksconstraints_comp.

import dolfin as df
import meshio
import numpy as np
import pygmsh
import scipy.sparse
from scipy import spatial

import openmdao.api as om

from atomics.api import PDEProblem, AtomicsGroup
from atomics.pdes.thermo_mechanical_mix_2d_stress import get_residual_form
from atomics.general_filter_comp import GeneralFilterComp

from atomics.extract_comp import ExtractComp
from atomics.ksconstraints_comp import KSConstraintsComp

'''
1. Define constants
'''

# objective = 'mass'
objective = 'compliance'
# objective = 'mass' or 'compliance'

# parameters for box
LENGTH  =  20.0e-2
WIDTH   =  20.0e-2
HIGHT   =  5.e-2
START_X = -10.0e-2
START_Y = -10.0e-2
START_Z = -2.5e-2

# parameters for cylindars (cells)
num_cell_x   =  5
num_cell_y   =  5
num_cells = num_cell_x*num_cell_y
first_cell_x = -8e-2
first_cell_y = -8e-2
end_cell_x   =  8e-2
end_cell_y   =  8e-2
x = np.linspace(first_cell_x, end_cell_x, num_cell_x)
y = np.linspace(first_cell_y, end_cell_y, num_cell_y)
xv, yv = np.meshgrid(x, y)
radius       =  0.01
axis_cell    = [0.0, 0.0, HIGHT]
A_cell = np.pi * (radius)**2
A_whole = (LENGTH * WIDTH)
cell_A_ratio = A_cell*(num_cell_x*num_cell_y)/A_whole

A_cell_quart = A_cell*(num_cell_x*num_cell_y) / 4
A_whole_quart = (LENGTH * WIDTH)/4

A_actual = 4.5e-3
A_now = A_whole_quart - A_cell_quart
ratio_act = A_actual / A_now
# constants for temperature field
KAPPA = 235
AREA_CYLINDER = 2 * np.pi * radius * HIGHT
AREA_SIDE = WIDTH * HIGHT
POWER = 90.
T_0 = 20.
q = df.Constant((POWER/AREA_CYLINDER)) # bdry heat flux
q_half = df.Constant((POWER/AREA_CYLINDER))
q_quart = df.Constant((POWER/AREA_CYLINDER))

# constants for thermoelastic model
K = 69e9
# K = 69e6
ALPHA = 13e-6
f_l = df.Constant(( 1.e6/AREA_SIDE, 0.))
f_r = df.Constant((-1.e6/AREA_SIDE, 0.))
f_b = df.Constant(( 0.,  1.e6/AREA_SIDE))
f_t = df.Constant(( 0., -1.e6/AREA_SIDE))



# f_l = df.Constant(( 0., 0.))
# f_r = df.Constant((0., 0.))
# f_b = df.Constant(( 0.,  0.))
# f_t = df.Constant(( 0., 0.))

1.2. Define the mesh

'''
2. Define mesh
'''
#-----------------Generate--mesh----------------
with pygmsh.occ.Geometry() as geom:
    geom.characteristic_length_min = 0.002
    geom.characteristic_length_max = 0.002
    disk_dic = {}
    disks = []

    rectangle = geom.add_rectangle([START_X, START_Y, 0.], LENGTH, WIDTH)
    for i in range(num_cells):
        name = 'disk' + str(i)
        disk_dic[name] = geom.add_disk([xv.flatten()[i], yv.flatten()[i], 0.], radius)
        disks.append(disk_dic[name])

    rectangle_1 = geom.add_rectangle([START_X, START_Y, 0.], LENGTH, WIDTH/2)
    rectangle_2 = geom.add_rectangle([START_X, 0., 0.], LENGTH/2, WIDTH/2)
    geom.boolean_difference(rectangle, geom.boolean_union([disks, rectangle_1, rectangle_2]))


    mesh = geom.generate_mesh()
    mesh.write("test_2d.vtk")


#-----------------read--mesh-------------
filename = 'test_2d.vtk'
mesh = meshio.read(
    filename,
    file_format="vtk"
)
points = mesh.points
cells = mesh.cells
meshio.write_points_cells(
    "test_2d.xml",
    points,
    cells,
    )

import os
os.system('gmsh -2 test_2d.vtk -format msh2')
os.system('dolfin-convert test_2d.msh mesh_2d.xml')
mesh = df.Mesh("mesh_2d.xml")

import matplotlib.pyplot as plt
plt.figure(1)

df.plot(mesh)
# plt.show()

'''
3. Define traction bc subdomains
'''

#-----------define-heating-boundary-------
class HeatBoundaryAll(df.SubDomain):
    def inside(self, x, on_boundary):
        cond_list = []
        for i in range(num_cells):
            cond = (abs(( x[0]-(xv.flatten()[i]) )**2 + ( x[1]-(yv.flatten()[i]) )**2) < (radius**2) + df.DOLFIN_EPS)
            cond_list = cond_list or cond
        return cond_list

class HeatBoundary(df.SubDomain):
    def inside(self, x, on_boundary):
        cond_list = []
        for i in [24, 23, 19, 18]:
            cond = (abs(( x[0]-(xv.flatten()[i]) )**2 + ( x[1]-(yv.flatten()[i]) )**2) < (radius**2) + df.DOLFIN_EPS)
            cond_list = cond_list or cond
        return cond_list

class HalfHeatBoundary(df.SubDomain):
    def inside(self, x, on_boundary):
        cond_list = []
        for i in [22, 17, 14, 13]:
            cond = (abs(( x[0]-(xv.flatten()[i]) )**2 + ( x[1]-(yv.flatten()[i]) )**2) < (radius**2) + df.DOLFIN_EPS)
            cond_list = cond_list or cond
        return cond_list

class QuartHeatBoundary(df.SubDomain):
    def inside(self, x, on_boundary):
        return (abs(( x[0] - 0.)**2 + ( x[1] - 0.)**2) < (radius**2) + df.DOLFIN_EPS)

#-----------define-surrounding-heat-sink-boundary-------
class SurroundingBoundary(df.SubDomain):
    def inside(self, x, on_boundary):
        return (
                # abs(x[0] -   START_X)  < df.DOLFIN_EPS or
                abs(x[0] - (-START_X)) < df.DOLFIN_EPS or
                # abs(x[1] -   START_Y)  < df.DOLFIN_EPS or
                abs(x[1] - (-START_Y)) < df.DOLFIN_EPS)

# Mark the HeatBoundary ass dss(6)
sub_domains = df.MeshFunction('size_t', mesh, mesh.topology().dim() - 1)
heat_edge_all = HeatBoundaryAll()
heat_edge = HeatBoundary()
heat_edge_half = HalfHeatBoundary()
heat_edge_quarter = QuartHeatBoundary()

heat_edge_all.mark(sub_domains, 4)
heat_edge.mark(sub_domains, 5)
heat_edge_half.mark(sub_domains, 6)
heat_edge_quarter.mark(sub_domains, 7)

class MidHBoundary(df.SubDomain):
    def inside(self, x, on_boundary):
        return (abs(x[1] )< df.DOLFIN_EPS)
class MidVBoundary(df.SubDomain):
    def inside(self, x, on_boundary):
        return (abs(x[0] )< df.DOLFIN_EPS)

class RightBoundary(df.SubDomain):
    def inside(self, x, on_boundary):
        return (abs(x[0] + START_X)< df.DOLFIN_EPS)

class BottomBoundary(df.SubDomain):
    def inside(self, x, on_boundary):
        return (abs(x[1] - START_Y)< df.DOLFIN_EPS)

class TopBoundary(df.SubDomain):
    def inside(self, x, on_boundary):
        return (abs(x[1] + START_Y)< df.DOLFIN_EPS)



# Mark the traction boundaries 8 10 12 14
# sub_domains = df.MeshFunction('size_t', mesh, mesh.topology().dim() - 1)
# left_edge  = LeftBoundary()
right_edge = RightBoundary()
# bottom_edge = BottomBoundary()
top_edge = TopBoundary()
# left_edge.mark(sub_domains, 8)
right_edge.mark(sub_domains, 10)
# bottom_edge.mark(sub_domains, 12)
top_edge.mark(sub_domains, 14)

dss = df.Measure('ds')(subdomain_data=sub_domains)

df.File('solutions_2d/domains_quart.pvd') << sub_domains

1.3. Define the PDE problem

# PDE problem
pde_problem = PDEProblem(mesh)

'''
Add input to the PDE problem
'''
# name = 'density', function = density_function (function is the solution vector here)
density_function_space = df.FunctionSpace(mesh, 'DG', 0)
density_function = df.Function(density_function_space)
pde_problem.add_input('density', density_function)

'''
Add states
'''
# Define mixed function space-split into temperature and displacement FS
d = mesh.geometry().dim()
cell = mesh.ufl_cell()
displacement_fe = df.VectorElement("CG",cell,1)
temperature_fe = df.FiniteElement("CG",cell,1)

mixed_fs = df.FunctionSpace(mesh, df.MixedElement([displacement_fe,temperature_fe]))
mixed_fs.sub(1).dofmap().dofs()
mixed_function = df.Function(mixed_fs)
displacements_function,temperature_function = df.split(mixed_function)

v,T_hat = df.TestFunctions(mixed_fs)

residual_form = get_residual_form(
    displacements_function,
    v,
    density_function,
    temperature_function,
    T_hat,
    KAPPA,
    K,
    ALPHA
)

residual_form -=  (df.dot(f_r, v) * dss(10) + df.dot(f_t, v) * dss(14)  + \
                    q*T_hat*dss(5) + q_half*T_hat*dss(6) + q_quart*T_hat*dss(7))
print("get residual_form-------")
pde_problem.add_state('mixed_states', mixed_function, residual_form, 'density')

'''
Add outputs
'''

# Add output-avg_density to the PDE problem:
volume = df.assemble(df.Constant(1.) * df.dx(domain=mesh))
avg_density_form = density_function / (df.Constant(1. * volume)) * df.dx(domain=mesh)
pde_problem.add_scalar_output('avg_density', avg_density_form, 'density')
print("Add output-avg_density-------")

# Add output-compliance to the PDE problem:

compliance_form = df.dot(f_r, displacements_function) * dss(10) +\
                    df.dot(f_t, displacements_function) * dss(14)
pde_problem.add_scalar_output('compliance', compliance_form, 'mixed_states')
print("Add output-compliance-------")

compliance_form = df.dot(f_r, displacements_function) * dss(10) +\
                    df.dot(f_t, displacements_function) * dss(14)
pde_problem.add_scalar_output('compliance', compliance_form, 'mixed_states')
print("Add output-compliance-------")


# Add output-compliance to the PDE problem:
C = density_function/(1 + 8. * (1. - density_function))

E = K * C # C is the design variable, its values is from 0 to 1

nu = 0.3 # Poisson's ratio
lambda_ = E * nu/(1. + nu)/(1 - 2 * nu)
mu = E / 2 / (1 + nu) #lame's parameters

lambda_ = 2*mu*lambda_/(lambda_+2*mu)
I = df.Identity(len(displacements_function))
T = df.TensorFunctionSpace(mesh, "CG", 1)
# T.vector.set_local()

w_ij = 0.5 * (df.grad(displacements_function) + df.grad(displacements_function).T) - ALPHA * I * temperature_function
sigm = lambda_*df.div(displacements_function)* I + 2*mu*w_ij
s = sigm - (1./3)*df.tr(sigm)*I
von_Mises = df.sqrt(3./2*df.inner(s/5e9, s/5e9) )
von_Mises_form = (1/df.CellVolume(mesh)) * von_Mises * df.TestFunction(density_function_space) * df.dx
pde_problem.add_field_output('von_Mises', von_Mises_form, 'mixed_states', 'density')


'''
Add bcs
'''

bc_displacements = df.DirichletBC(mixed_fs.sub(0).sub(0), df.Constant((0.0)), MidVBoundary())
bc_displacements_1 = df.DirichletBC(mixed_fs.sub(0).sub(1), df.Constant((0.0)), MidHBoundary())

bc_temperature = df.DirichletBC(mixed_fs.sub(1), df.Constant(T_0), SurroundingBoundary())

# Add boundary conditions to the PDE problem:
pde_problem.add_bc(bc_displacements)
pde_problem.add_bc(bc_displacements_1)
pde_problem.add_bc(bc_temperature)

'''
'''
coords = density_function_space.tabulate_dof_coordinates()
tree = spatial.cKDTree(coords)
idx_list = []
plt.figure(2)
for i in [12, 13, 14 , 17, 18, 19, 22, 23, 24]:
    idx = tree.query_ball_point(list(np.array([xv.flatten()[i], yv.flatten()[i]])), radius+2e-3)
    idx_list.extend(idx)
nearest_points = coords[idx_list]
plt.gca().set_aspect('equal', adjustable='box')
plt.plot(nearest_points[:,0],nearest_points[:,1],'bo')


# plt.figure(3)
x = []
y = []
idx_rec = []
x_line = y_line = np.linspace(0, 0.1, num=100)
x_0 = y_0 = np.zeros(100)
x_1 = y_1 = np.ones(100) * 0.1
x.extend(x_1)
x.extend(x_line)

y.extend(y_line)
y.extend(y_1)

plt.gca().set_aspect('equal', adjustable='box')

for i in range(len(x)):
    idx = tree.query_ball_point(list(np.array([x[i], y[i]])), 3e-3)
    idx_rec.extend(idx)
nearest_points_rec = coords[idx_rec]
plt.plot(nearest_points_rec[:,0],nearest_points_rec[:,1],'go')

# plt.plot([x_line, x_1, x_line, x_0],[y_0, y_line, y_1, y_line],'bo')
plt.show()

idx_list.extend(idx_rec)
lower_bd = np.ones(coords[:,0].size)*1e-5
idx_list_norepeat = []
for i in idx_list:
    if i not in idx_list_norepeat:
        idx_list_norepeat.append(i)
idx_array = np.asarray(idx_list_norepeat)
lower_bd[idx_array] = 1.

1.4. Set up the OpenMDAO model

# Define the OpenMDAO problem and model

prob = om.Problem()

num_dof_density = pde_problem.inputs_dict['density']['function'].function_space().dim()

comp = om.IndepVarComp()
comp.add_output(
    'density_unfiltered',
    shape=num_dof_density,
    val=np.ones(num_dof_density),
    # val=np.random.random(num_dof_density) * 0.86,
)
prob.model.add_subsystem('indep_var_comp', comp, promotes=['*'])

print('indep_var_comp')

comp = GeneralFilterComp(density_function_space=density_function_space)
prob.model.add_subsystem('general_filter_comp', comp, promotes=['*'])
print('general_filter_comp')


group = AtomicsGroup(pde_problem=pde_problem)
prob.model.add_subsystem('atomics_group', group, promotes=['*'])
print('atomics_group')

comp = ExtractComp(
    in_name='mixed_states',
    out_name='temperature_field',
    in_shape=pde_problem.states_dict['mixed_states']['function'].function_space().dim(),
    partial_dof=np.array(mixed_fs.sub(1).dofmap().dofs()),
)
prob.model.add_subsystem('ExtractComp', comp, promotes=['*'])
print('ExtractComp')

comp = KSConstraintsComp(
    in_name='temperature_field',
    out_name='t_max',
    shape=(np.array(mixed_fs.sub(1).dofmap().dofs()).size,),
    axis=0,
    # rho=50.,
    rho=10,
)
prob.model.add_subsystem('KSConstraintsComp', comp, promotes=['*'])
print('KSConstraintsComp')

comp = KSConstraintsComp(
    in_name='von_Mises',
    out_name='von_Mises_max',
    shape=(np.array(density_function_space.dofmap().dofs()).size,),
    axis=0,
    # rho=50.,
    rho=40.,
)
prob.model.add_subsystem('KSConstraintsstress', comp, promotes=['*'])



prob.model.add_design_var('density_unfiltered',upper=1., lower=1e-4)

if objective == 'mass':
    prob.model.add_objective('avg_density')
    prob.model.add_constraint('t_max', upper=50)
    prob.model.add_constraint('density', upper=1.,lower=1.,
                            indices=idx_array, linear=True)
else:
    prob.model.add_objective('compliance')
    prob.model.add_constraint('avg_density', upper=0.80, linear=True)
    prob.model.add_constraint('t_max', upper=50)
    prob.model.add_constraint('density',upper=1.,lower=1.,
                                indices=idx_array, linear=True)

# prob.model.add_objective('compliance')
# prob.model.add_constraint('von_Mises_max', upper=10)
# prob.model.add_constraint('avg_density', upper=0.75, linear=True)
# prob.model.add_constraint('t_max', upper=55)
# prob.model.add_constraint('density',upper=1.,lower=1.,
#                              indices=idx_array, linear=True)


prob.driver = driver = om.pyOptSparseDriver()
driver.options['optimizer'] = 'SNOPT'
driver.opt_settings['Verify level'] = 0
driver.opt_settings['Major iterations limit'] = 10000
driver.opt_settings['Minor iterations limit'] = 1000000
driver.opt_settings['Iterations limit'] = 100000000
driver.opt_settings['Major step limit'] = 2.0

driver.opt_settings['Major feasibility tolerance'] = 1.0e-5
driver.opt_settings['Major optimality tolerance'] =2.e-10

prob.setup()

prob.run_driver()

displacements_function_val, temperature_function_val= mixed_function.split()
'solutions/case_1/cantilever_beam/displacement.pvd'
#save the solution vector
df.File('solutions/case_2/battter_pack_{}/displacements.pvd'.format(objective)) << displacements_function_val
df.File('solutions/case_2/battter_pack_{}/temperature.pvd'.format(objective)) << temperature_function_val
df.File('solutions/case_2/battter_pack_{}/density.pvd'.format(objective)) << density_function
stiffness  = df.project(density_function/(1 + 8. * (1. - density_function)), density_function_space)
df.File('solutions/case_2/battter_pack_{}/stiffness.pvd'.format(objective)) << stiffness

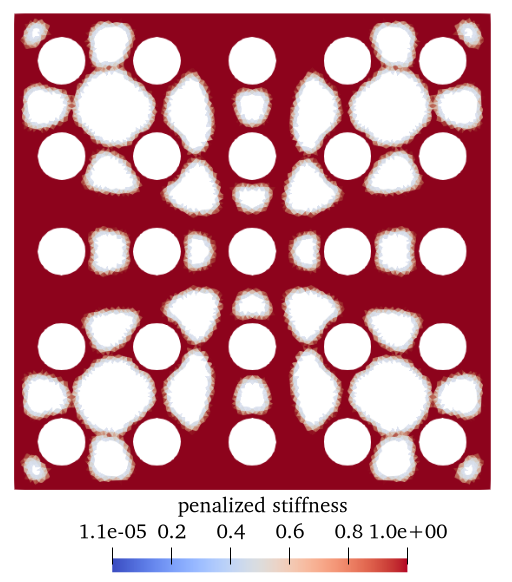
2. Results (density plot)

The users can visualize the optimized densities by opening the <name>.pvd from Paraview.